Transformations
Précédemment dans ce tutoriel, nous avons étudié la grille du canevas et le système de coordonnées. Jusqu'à maintenant, nous avons uniquement utilisé la grille par défaut et modifié la taille de la globalité du canevas afin de répondre à nos besoins. Les transformations que nous allons aborder dans la suite vont nous permettre, de manière plus puissante, d'effectuer des déplacements et des rotations sur la grille et même d'effectuer des mises à l'échelle.
Sauvegarde et restauration d'état
Avant d'étudier les méthodes de transformations, examinons deux autres méthodes qui vont être indispensables à partir du moment où l'on commence à créer des dessins complexes.
save()-
Sauvegarde l'état du canevas dans sa globalité.
restore()-
Restore le plus récent état sauvegardé du canevas.
Les états du canevas sont stockés dans une pile. Chaque invocation de la méthode save() ajoute une copie de l'état courant du canevas en haut de la pile. L'état du dessin est constitué de :
- les transformations qui ont été appliquées (exemples : déplacement, rotation, mise à l'échelle).
- Les valeurs actuelles des attributs suivants :
strokeStyle,fillStyle,globalAlpha,lineWidth,lineCap,lineJoin,miterLimit,lineDashOffset,shadowOffsetX,shadowOffsetY,shadowBlur,shadowColor,globalCompositeOperation,font,textAlign,textBaseline,direction,imageSmoothingEnabled. - Le chemin de découpe (clipping path) actuel, qu'on abordera plus loin.
La méthode save() peut être invoquée autant de fois que nécessaire. Chaque appel de restore() enlève le dernier état sauvegardé de la pile et tous les paramètres sauvegardés sont restaurés.
Un exemple de sauvegarde et de restauration de l état du canevas
Cet exemple tente d'illustrer comment fonctionne la pile d'états de dessin en dessinant un ensemble de rectangles consécutifs.
function draw() {
var ctx = document.getElementById("canvas").getContext("2d");
ctx.fillRect(0, 0, 150, 150); // Dessine un rectangle avec les réglages par défaut
ctx.save(); // Sauvegarde l'état par défaut
ctx.fillStyle = "#09F"; // Fait des changements de réglages
ctx.fillRect(15, 15, 120, 120); // Dessine un rectangle avec les nouveaux réglages
ctx.save(); // Sauvegarde l'état actuel
ctx.fillStyle = "#FFF"; // Fait des changements de réglages
ctx.globalAlpha = 0.5;
ctx.fillRect(30, 30, 90, 90); // Dessine un rectangle avec de nouveaux réglages
ctx.restore(); // Restaure l'état précédent
ctx.fillRect(45, 45, 60, 60); // Dessine un rectangle avec les réglages restaurés
ctx.restore(); // Restaure l'état d'origine
ctx.fillRect(60, 60, 30, 30); // Dessine un rectangle avec les réglages restaurés
}
La première étape consiste à dessiner un grand rectangle avec les paramètres par défaut. Ensuite, nous sauvegardons cet état et modifions la couleur de remplissage. Nous dessinons ensuite le deuxième rectangle bleu et mettons l'état de côté. Encore une fois, nous modifions certains paramètres de dessin et dessinons le troisième rectangle blanc semi-transparent.
Jusqu'à présent, cela ressemble beaucoup à ce que nous avons fait dans les sections précédentes. Cependant, une fois que nous appelons la première instruction restore(), l'état de dessin supérieur est supprimé de la pile et les paramètres sont restaurés. Si nous n'avions pas sauvegardé l'état en utilisant save (), nous devrions modifier manuellement la couleur de remplissage et la transparence afin de revenir à l'état précédent. Cela serait facile pour deux propriétés, mais si nous avons plus que cela, notre code deviendrait très long très rapidement.
Lorsque la deuxième instruction restore() est appelée, l'état d'origine (celui que nous avons configuré avant le premier appel à enregistrer) est restauré et le dernier rectangle est de nouveau tracé en noir.
Déplacement
La première des méthodes de transformation que nous examinerons est translate (). Cette méthode est utilisée pour déplacer la toile et son origine vers un autre point de la grille.
translate(x, y)-
Déplace la toile et son origine sur la grille.
xindique la distance horizontale du déplacement, etyindique à quelle distance déplacer la grille verticalement.

C'est une bonne idée de sauvegarder l'état du canevas avant d'effectuer des transformations. Dans la plupart des cas, il est plus facile d'appeler la méthode restore que d'avoir à effectuer un déplacement inverse pour revenir à l'état d'origine. De même, si vous déplacez à l'intérieur d'une boucle et que vous ne sauvegardez pas et ne restaurez pas l'état du canevas, il se peut qu'une partie de votre dessin soit manquante, car elle a été dessinée en dehors du bord du canevas.
Un exemple translate
Cet exemple montre certains des avantages du déplacement de l'origine du canevas. Sans la méthode translate(), tous les rectangles seraient dessinés à la même position (0,0). La méthode translate() nous donne également la liberté de placer le rectangle n'importe où sur le canevas sans avoir à ajuster manuellement les coordonnées dans la fonction fillRect(). Cela le rend un peu plus facile à comprendre et à utiliser.
Dans la fonction draw (), nous appelons la fonction fillRect () neuf fois en utilisant deux boucles for . Dans chaque boucle, le canevas est déplacé, le rectangle est dessiné et le canevas est retourné à son état d'origine. Notez comment l'appel à fillRect () utilise les mêmes coordonnées à chaque fois, en s'appuyant sur translate () pour ajuster la position du dessin.
function draw() {
var ctx = document.getElementById("canvas").getContext("2d");
for (var i = 0; i < 3; i++) {
for (var j = 0; j < 3; j++) {
ctx.save();
ctx.fillStyle = "rgb(" + 51 * i + ", " + (255 - 51 * i) + ", 255)";
ctx.translate(10 + j * 50, 10 + i * 50);
ctx.fillRect(0, 0, 25, 25);
ctx.restore();
}
}
}
Rotation
La seconde méthode de transformation est rotate(). Nous l'utilisons pour faire pivoter le canevas autour de l'origine actuelle.
rotate(angle)-
Fait pivoter le canevas, dans le sens des aiguilles d'une montre autour de l'origine actuelle, par le nombre de radians de l'angle.
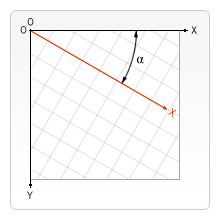
Le point central de rotation est toujours l'origine de la toile. Pour changer le point central, nous devrons déplacer le canevas en utilisant la méthode translate ().
Un exemple rotate
Dans cet exemple, nous utiliserons la méthode rotate () pour faire d'abord tourner un rectangle à partir de l'origine du canevas, puis du centre du rectangle lui-même à l'aide de translate ().
Note :
Les angles sont en radians, pas en degrés. Pour convertir en degrés, nous utilisons : radians = (Math.PI/180)*degrees.
function draw() {
var ctx = document.getElementById("canvas").getContext("2d");
// rectangles de gauche, rotation depuis l'origine du canevas
ctx.save();
// rectangle bleu
ctx.fillStyle = "#0095DD";
ctx.fillRect(30, 30, 100, 100);
ctx.rotate((Math.PI / 180) * 25);
// rectangle gris
ctx.fillStyle = "#4D4E53";
ctx.fillRect(30, 30, 100, 100);
ctx.restore();
// rectangles de droite, rotation depuis le centre du rectangle
// dessine le rectangle bleu
ctx.fillStyle = "#0095DD";
ctx.fillRect(150, 30, 100, 100);
ctx.translate(200, 80); // déplace au centre du rectangle
// x = x + 0.5 * width
// y = y + 0.5 * height
ctx.rotate((Math.PI / 180) * 25); // rotation
ctx.translate(-200, -80); // déplace en arrière
// dessine le rectangle gris
ctx.fillStyle = "#4D4E53";
ctx.fillRect(150, 30, 100, 100);
}
Pour faire pivoter le rectangle autour de son propre centre, nous déplaçons le canevas au centre du rectangle, puis faisons pivoter le canevas, puis le déplaçons à 0,0, puis dessinons le rectangle.
Mise à l'échelle
La méthode de transformation suivante est la mise à l'échelle. Nous l'utilisons pour augmenter ou diminuer les unités de notre grille de canevas. Cela peut être utilisé pour dessiner des formes ou des bitmaps réduits ou agrandis.
scale(x, y)-
Met à l'échelle les unités du canevas avec x horizontalement et y verticalement. Les deux paramètres sont des nombres réels. Les valeurs inférieures à 1,0 réduisent la taille de l'unité et les valeurs supérieures à 1,0 augmentent la taille de l'unité. Les valeurs 1.0 laissent les unités à la même taille.
En utilisant des nombres négatifs, vous pouvez faire une mise en miroir d'axe (par exemple en utilisant translate (0, canvas.height), scale (1, -1), vous aurez le système de coordonnées cartésien bien connu, avec l'origine dans le coin inférieur gauche).
Par défaut, une unité sur la toile est exactement un pixel. Si nous appliquons, par exemple, un facteur d'échelle de 0,5, l'unité résultante deviendrait 0,5 pixels et ainsi les formes seraient dessinées à la moitié de la taille. De la même façon, si nous définissons le facteur d'échelle sur 2.0, la taille de l'unité augmentera et une unité deviendra deux pixels. Cela donne des formes dessinées deux fois plus grandes.
Un exemple scale
Dans ce dernier exemple, nous allons dessiner des formes avec différents facteurs d'échelle.
function draw() {
var ctx = document.getElementById("canvas").getContext("2d");
// dessine un rectangle simple, mais le met à l'échelle.
ctx.save();
ctx.scale(10, 3);
ctx.fillRect(1, 10, 10, 10);
ctx.restore();
// mirror horizontally
ctx.scale(-1, 1);
ctx.font = "48px serif";
ctx.fillText("MDN", -135, 120);
}
Transformation
Enfin, les méthodes de transformation suivantes appliquent des modifications directement à la matrice de transformation.
transform(a, b, c, d, e, f)-
Multiplie la matrice de transformation actuelle avec la matrice décrite par ses arguments. La matrice de transformation est décrite par :
Si l'un des arguments est
infini, la matrice de transformation doit être marquée comme infinie, plutôt que d'utiliser la méthode qui lance une exception.
Les paramètres de cette fonction sont :
a (m11)-
Mise à l'échelle horizontale.
b (m12)-
Inclinaison horizontale.
c (m21)-
Inclinaison verticale.
d (m22)-
Mise à l'échelle verticale.
e (dx)-
Déplacement horizontal.
f (dy)-
Déplacement vertical.
setTransform(a, b, c, d, e, f)-
Réinitialise la transformation en cours dans la matrice d'identité, puis appelle la méthode
transform ()avec les mêmes arguments. Cela défait la transformation en cours, puis définit la transformation spécifiée, le tout en une seule étape. resetTransform()-
Réinitialise la transformation en cours à la matrice d'identité. C'est la même chose que d'appeler :
ctx.setTransform (1, 0, 0, 1, 0, 0);
Exemple pour transform et setTransform
function draw() {
var ctx = document.getElementById("canvas").getContext("2d");
var sin = Math.sin(Math.PI / 6);
var cos = Math.cos(Math.PI / 6);
ctx.translate(100, 100);
var c = 0;
for (var i = 0; i <= 12; i++) {
c = Math.floor((255 / 12) * i);
ctx.fillStyle = "rgb(" + c + ", " + c + ", " + c + ")";
ctx.fillRect(0, 0, 100, 10);
ctx.transform(cos, sin, -sin, cos, 0, 0);
}
ctx.setTransform(-1, 0, 0, 1, 100, 100);
ctx.fillStyle = "rgba(255, 128, 255, 0.5)";
ctx.fillRect(0, 50, 100, 100);
}