變形效果

畫布狀態儲存與復原

在使用變形效果等複雜繪圖方法之前，有兩個不可或缺的方法(method)必須要先了解一下:

save()

儲存現階段畫布完整狀態。

restore()

復原最近一次儲存的畫布狀態。

每一次呼叫 save()，畫布狀態便會存進一個堆疊(stack)之中。畫布狀態包含了:

  • 曾經套用過的變形效果，如 translate, rotate 和 scale(稍後說明)。
  • strokeStyle, fillStyle, globalAlpha, lineWidth, lineCap, lineJoin, miterLimit, shadowOffsetX, shadowOffsetY, shadowBlur, shadowColor, globalCompositeOperation 屬性的屬性值
  • 目前截圖路徑(稍後說明)。

我們可以呼叫 save()的次數不限，而每一次呼叫 restore()，最近一次儲存的畫布狀態便會從堆疊中被取出，然後還原畫布到此畫布狀態。

畫布狀態儲存與復原範例

本例會畫一連串矩形圖案來說明畫布狀態堆疊是如何運作。

function draw() {
  var ctx = document.getElementById('canvas').getContext('2d');

  ctx.fillRect(0,0,150,150);   // Draw a rectangle with default settings
  ctx.save();                  // Save the default state

  ctx.fillStyle = '#09F'       // Make changes to the settings
  ctx.fillRect(15,15,120,120); // Draw a rectangle with new settings

  ctx.save();                  // Save the current state
  ctx.fillStyle = '#FFF'       // Make changes to the settings
  ctx.globalAlpha = 0.5;
  ctx.fillRect(30,30,90,90);   // Draw a rectangle with new settings

  ctx.restore();               // Restore previous state
  ctx.fillRect(45,45,60,60);   // Draw a rectangle with restored settings

  ctx.restore();               // Restore original state
  ctx.fillRect(60,60,30,30);   // Draw a rectangle with restored settings
}

預設用黑色填滿這個矩形

每種狀態可以看成是一層層堆疊的步驟紀錄

第一步：畫出黑色矩形 接著把第一個狀態儲存下來(用黑色填滿)

第二步：畫出藍色矩形 接著把第二個狀態儲存下來(用藍色填滿)

第三步：畫出半透明矩形

第四步：再畫出矩形 這時候我們取用最新儲存過的藍色(第二狀態)

第五步：再畫一個矩形 我們再取出更早之前儲存的黑色(第一狀態)

ScreenshotLive sample

移動畫布

第一個變形效果方法是 translate()。translate()是用來移動畫布，如右圖，原先畫布的原點在網格(0, 0)位置，我們可以移動畫布，使其原點移到(x, y)位置。

translate(x, y)

移動網格上的畫布，其中 x 代表水平距離、y 代表垂直距離。

最好在做任何變形效果前先儲存一下畫布狀態，如此當我們需要復原先前的狀態時，只需要呼叫一下 restore()即可，而且有一種情況是當我們在迴圈中移動畫布，如果不記得儲存和回復畫布狀態，繪圖區域很容易最後就超出邊界，然後出現圖案不見的狀況。

移動畫布範例

下面程式碼示範了利用 translate()畫圖的好處，裡面，我們用了 drawSpirograph()函數畫萬花筒類的圖案，如果沒有移動畫布原點，那麼每個圖案只會有四分之一會落在可視範圍，藉由移動畫布原點我們便可以自由變換每個圖案的位置，使圖案完整出現，而且省去手動計算調整每個圖案的座標位置。

另外一個 draw()函數透過兩個 for 迴圈移動畫布原點、呼叫 drawSpirograph()函數、復歸畫布圓點位置共九次。

function draw() {
  var ctx = document.getElementById('canvas').getContext('2d');
  ctx.fillRect(0,0,300,300);
  for (var i=0;i<3;i++) {
    for (var j=0;j<3;j++) {
      ctx.save();
      ctx.strokeStyle = "#9CFF00";
      ctx.translate(50+j*100,50+i*100);
      drawSpirograph(ctx,20*(j+2)/(j+1),-8*(i+3)/(i+1),10);
      ctx.restore();
    }
  }
}

function drawSpirograph(ctx,R,r,O){
  var x1 = R-O;
  var y1 = 0;
  var i  = 1;
  ctx.beginPath();
  ctx.moveTo(x1,y1);
  do {
    if (i>20000) break;
    var x2 = (R+r)*Math.cos(i*Math.PI/72) - (r+O)*Math.cos(((R+r)/r)*(i*Math.PI/72))
    var y2 = (R+r)*Math.sin(i*Math.PI/72) - (r+O)*Math.sin(((R+r)/r)*(i*Math.PI/72))
    ctx.lineTo(x2,y2);
    x1 = x2;
    y1 = y2;
    i++;
  } while (x2 != R-O && y2 != 0 );
  ctx.stroke();
}
ScreenshotLive sample

旋轉

rotate()函數可以畫布原點作中心，旋轉畫布。

rotate(x)

以畫布原點為中心，順時針旋轉畫布 x 弧度(弧度 = Math.PI * 角度 / 180)。

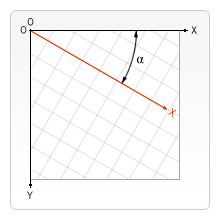
我們可以呼叫 translate()方法來移動旋轉中心(亦即畫布原點)。

旋轉範例

本範例我們呼叫 rotate()方法來畫一系列環狀圖案。如果不用 rotate()，同樣的效果也可以藉由個別計算 x, y 座標點(x = r*Math.cos(a); y = r*Math.sin(a))達成；呼叫 rotate()和個別計算 x, y 座標點不同之處在於，個別計算 x, y 座標點只有旋轉圓形圓心，而圓形並沒有旋轉，呼叫 rotate()則會旋轉圓形和圓心，不過因為我們的圖案是圓形，所以兩種作法產生的效果不會有差異。

我們執行了兩個迴圈來作圖，第一個迴圈決定的圓環個數和該圓環上圓環上圓點的個數的顏色，第二個迴圈決定了圓環上圓點的個數，每一次作圖前我們都儲存了原始畫布狀態，以便結束時可以復原狀態。畫布旋轉的弧度則以圓環上圓點的個數決定，像是最內圈的圓環共有六個圓點，所以每畫一個原點，畫布就旋轉 60 度(360 度/6)，第二的圓環有 12 個原點，所以畫布一次旋轉度數為 30 度(360 度/12)，以此類推。

function draw() {
  var ctx = document.getElementById('canvas').getContext('2d');
  ctx.translate(75,75);

  for (var i=1;i<6;i++){ // Loop through rings (from inside to out)
    ctx.save();
    ctx.fillStyle = 'rgb('+(51*i)+','+(255-51*i)+',255)';

    for (var j=0;j<i*6;j++){ // draw individual dots
      ctx.rotate(Math.PI*2/(i*6));
      ctx.beginPath();
      ctx.arc(0,i*12.5,5,0,Math.PI*2,true);
      ctx.fill();
    }

    ctx.restore();
  }
}
ScreenshotLive sample

縮放

接下來這一個變形效果為縮放圖形。

scale(x, y)

x 代表縮放畫布水平網格單位 x 倍，y 代表縮放畫布垂直網格單位 y 倍，輸入 1.0 不會造成縮放。如果輸入負值會造成座標軸鏡射，假設輸入 x 為-1，那麼原本畫布網格 X 軸上的正座標點都會變成負座標點、負座標點則變成正座標點。

只要利用 scale()，我們可以建立著名的笛卡兒座標系；執行 translate(0,canvas.height)先移動畫布原點到左下角，再執行 scale(1,-1)顛倒 Y 軸正負值，一個笛卡兒座標系便完成了。

預設上畫布網格前進一單位等於前進一像素大小，所以縮小 0.5 倍，就會變成前進 0.5 的像素大小，亦即縮小圖像一半大小，反之，放大 2 倍將放大圖像 2 倍。

縮放範例

本程式碼範例會畫出一系列不同縮放比例的萬花筒樣式圖案。

function draw() {
  var ctx = document.getElementById('canvas').getContext('2d');
  ctx.strokeStyle = "#fc0";
  ctx.lineWidth = 1.5;
  ctx.fillRect(0,0,300,300);

  // Uniform scaling
  ctx.save()
  ctx.translate(50,50);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(100,0);
  ctx.scale(0.75,0.75);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(133.333,0);
  ctx.scale(0.75,0.75);
  drawSpirograph(ctx,22,6,5);
  ctx.restore();

  // Non uniform scaling (y direction)
  ctx.strokeStyle = "#0cf";
  ctx.save()
  ctx.translate(50,150);
  ctx.scale(1,0.75);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(100,0);
  ctx.scale(1,0.75);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(100,0);
  ctx.scale(1,0.75);
  drawSpirograph(ctx,22,6,5);
  ctx.restore();

  // Non uniform scaling (x direction)
  ctx.strokeStyle = "#cf0";
  ctx.save()
  ctx.translate(50,250);
  ctx.scale(0.75,1);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(133.333,0);
  ctx.scale(0.75,1);
  drawSpirograph(ctx,22,6,5);

  ctx.translate(177.777,0);
  ctx.scale(0.75,1);
  drawSpirograph(ctx,22,6,5);
  ctx.restore();

}
function drawSpirograph(ctx,R,r,O){
  var x1 = R-O;
  var y1 = 0;
  var i  = 1;
  ctx.beginPath();
  ctx.moveTo(x1,y1);
  do {
    if (i>20000) break;
    var x2 = (R+r)*Math.cos(i*Math.PI/72) - (r+O)*Math.cos(((R+r)/r)*(i*Math.PI/72))
    var y2 = (R+r)*Math.sin(i*Math.PI/72) - (r+O)*Math.sin(((R+r)/r)*(i*Math.PI/72))
    ctx.lineTo(x2,y2);
    x1 = x2;
    y1 = y2;
    i++;
  } while (x2 != R-O && y2 != 0 );
  ctx.stroke();
}

第一排第一個黃色圖案是沒有縮放的圖案，然後往右到了第二個圖案，我們程式碼中輸入了 (0.75, 0.75)的縮放倍率，到了第三個圖案，我們還是輸入了 (0.75, 0.75)的縮放倍率，而基於之前有縮小過一次，所以第三個圖案相對於第一個沒有縮放的圖案是 0.75 × 0.75 = 0.5625 倍。

第二排藍色圖案我們只改變 Y 軸的縮放倍率，X 軸維持不變，因而產生一個比一個更扁的橢圓圖形。同理，第三排綠色圖案改變 X 軸的縮放倍率，Y 軸維持不變。

ScreenshotLive sample

變形

最後一個方法是設定變形矩陣，藉由改變變形矩陣，我們因此可以營造各種變形效果；其實先前所提到的 rotate, translate, scale 都是在設定變形矩陣，而這邊的這個方法就是直接去改變變形矩陣。

transform(m11, m12, m21, m22, dx, dy)

呼叫 Transform 會拿目前的變形矩陣乘以下列矩陣:plain m11 m21 dx m12 m22 dy 0 0 1 運算後的新矩陣將取代目前的變形矩陣。其中 m11 代表水平縮放圖像，m12 代表水平偏移圖像，m21 代表垂直偏移圖像，m22 代表垂直縮放圖像，dx 代表水平移動圖像，dy 代表垂直移動圖像。如果輸入Infinity 值，不會引起例外錯誤，矩陣值會依照輸入設成無限。

setTransform(m11, m12, m21, m22, dx, dy)

復原目前矩陣為恆等矩陣(Identiy matrix，也就是預設矩陣)，然後再以輸入參數呼叫 transform()。

transform / setTransform 範例

function draw() {
  var ctx = document.getElementById('canvas').getContext('2d');

  var sin = Math.sin(Math.PI/6);
  var cos = Math.cos(Math.PI/6);
  ctx.translate(100, 100);
  var c = 0;
  for (var i=0; i <= 12; i++) {
    c = Math.floor(255 / 12 * i);
    ctx.fillStyle = "rgb(" + c + "," + c + "," + c + ")";
    ctx.fillRect(0, 0, 100, 10);
    ctx.transform(cos, sin, -sin, cos, 0, 0);
  }

  ctx.setTransform(-1, 0, 0, 1, 100, 100);
  ctx.fillStyle = "rgba(255, 128, 255, 0.5)";
  ctx.fillRect(0, 50, 100, 100);
}
ScreenshotLive sample