Рисование фигур с помощью canvas

Теперь, установив наше окружение canvas, мы можем погрузиться в детали того, как рисовать в canvas. К концу этой статьи, вы научитесь рисовать прямоугольники, треугольники, линии, дуги и кривые, при условии что вы хорошо знакомы с основными геометрическими фигурами. Работа с путями весьма важна, когда рисуете объекты на canvas и мы увидим как это может быть сделано.

Сетка

Перед тем, как мы начнём рисовать, нам нужно поговорить о сетке canvas или координатной плоскости. Наш HTML каркас из предыдущей страницы включал в себя элемент canvas 150 пикселей в ширину и 150 пикселей в высоту. Справа можно увидеть этот canvas с сеткой, накладываемой по умолчанию. Обычно 1 единица на сетке соответствует 1 пикселю на canvas. Начало координат этой сетки расположено в верхнем левом углу в координате (0,0 ). Все элементы размещены относительно этого начала. Таким образом, положение верхнего левого угла синего квадрата составляет х пикселей слева и у пикселей сверху, на координате (х, у). Позже в этом уроке мы увидим, как можно перевести начало координат в другое место, вращать сетку и даже масштабировать её, но сейчас мы будем придерживаться настроек сетки по умолчанию.

Рисование прямоугольников

В отличие от SVG, <canvas> поддерживает только одну примитивную фигуру: прямоугольник. Все другие фигуры должны быть созданы комбинацией одного или большего количества контуров (paths), набором точек, соединённых в линии. К счастью в ассортименте рисования контуров у нас есть функции, которые делают возможным составление очень сложных фигур.

Сначала рассмотрим прямоугольник. Ниже представлены три функции рисования прямоугольников в canvas:

fillRect(x, y, width, height): Рисование заполненного прямоугольника.
strokeRect(x, y, width, height): Рисование прямоугольного контура.
clearRect(x, y, width, height): Очистка прямоугольной области, делая содержимое совершенно прозрачным.

Каждая из приведённых функций принимает несколько параметров:

x, y устанавливают положение верхнего левого угла прямоугольника в canvas (относительно начала координат);
width (ширина) и height (высота) определяют размеры прямоугольника.

Ниже приведена функция draw(), использующая эти три функции.

Пример создания прямоугольных фигур

<html>
  <body onload="draw();">
    <canvas id="canvas" width="150" height="150"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    ctx.fillRect(25, 25, 100, 100);
    ctx.clearRect(45, 45, 60, 60);
    ctx.strokeRect(50, 50, 50, 50);
  }
}

Этот пример изображён ниже.

Функция fillRect() рисует большой чёрный квадрат со стороной 100 px. Функция clearRect() вырезает квадрат 60х60 из центра, а функция strokeRect() создаёт прямоугольный контур 50х50 пикселей внутри очищенного квадрата.

На следующей странице мы рассмотрим две альтернативы методу clearRect(), и также увидим, как можно изменять цвет и стиль контура отображаемых фигур.

В отличие от функций создания контуров, которые будут рассмотрены в следующем разделе, все три функции создания прямоугольника сразу же отображаются на canvas.

Рисование контуров (path)

Остальные примитивные фигуры создаются контурами. Контур - это набор точек, которые, соединяясь в отрезки линий, могут образовывать различные фигуры, изогнутые или нет, разной ширины и разного цвета. Контур (или субконтур) может быть закрытым.

Создание фигур используя контуры происходит в несколько важных шагов:

Сначала вы создаёте контур.
Затем, используя команды рисования, рисуете контур.
Потом закрываете контур.
Созданный контур вы можете обвести или залить для его отображения.

Здесь приведены функции, которые можно использовать в описанных шагах:

beginPath(): Создаёт новый контур. После создания используется в дальнейшем командами рисования при построении контуров.
Path методы: Методы для установки различных контуров объекта.
closePath(): Закрывает контур, так что будущие команды рисования вновь направлены контекст.
stroke(): Рисует фигуру с внешней обводкой.
fill(): Рисует фигуру с заливкой внутренней области.

Первый шаг создания контура заключается в вызове функции beginPath(). Внутри содержатся контуры в виде набора суб-контуров (линии, дуги и др.), которые вместе образуют форму фигуры. Каждый вызов этого метода очищает набор, и мы можем начинать рисовать новые фигуры.

Примечание: Если текущий контур пуст (например, как после вызова beginPath() или на вновь созданном canvas), первой командой построения контура всегда является функция moveTo(). Поэтому мы всегда можем установить начальную позицию рисования контура после перезагрузки.

Вторым шагом является вызов методов, определяемых видом контура, который нужно нарисовать. Их мы рассмотрим позднее.

Третий и необязательный шаг - это вызов closePath(). Этот метод пытается закрыть фигуру, рисуя прямую линию из текущей точки в начальную. Если фигура была уже закрыта или является просто точкой, то функция ничего не делает.

Примечание: Когда вы вызываете fill(), то каждая открытая фигура закрывается автоматически, так что вы можете не использовать closePath(). Это обстоятельство не имеет место в случае вызова stroke().

Рисование треугольника

Например, код для рисования треугольника будет выглядеть как-то так:

<html>
  <body onload="draw();">
    <canvas id="canvas" width="100" height="100"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    ctx.beginPath();
    ctx.moveTo(75, 50);
    ctx.lineTo(100, 75);
    ctx.lineTo(100, 25);
    ctx.fill();
  }
}

Результат выглядит так:

Передвижение пера

Одна очень полезная функция, которая ничего не рисует, но связана по смыслу с вышеописанными функциями - это moveTo(). Вы можете представить это как отрыв (подъем) пера от бумаги и его перемещение в другое место.

moveTo(x, y): Перемещает перо в точку с координатами x и y.

При инициализации canvas или при вызове beginPath(), вы захотите использовать функцию moveTo() для перемещения в точку начала рисования. Можно использовать moveTo() и для рисования несвязанного(незакрытого) контура. Посмотрите на смайлик ниже.

Вы можете проверить это сами, используя участок кода ниже. Просто вставьте в функцию draw(), рассмотренную ранее.

<html>
  <body onload="draw();">
    <canvas id="canvas" width="150" height="150"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    ctx.beginPath();
    ctx.arc(75, 75, 50, 0, Math.PI * 2, true); // Внешняя окружность
    ctx.moveTo(110, 75);
    ctx.arc(75, 75, 35, 0, Math.PI, false); // рот (по часовой стрелке)
    ctx.moveTo(65, 65);
    ctx.arc(60, 65, 5, 0, Math.PI * 2, true); // Левый глаз
    ctx.moveTo(95, 65);
    ctx.arc(90, 65, 5, 0, Math.PI * 2, true); // Правый глаз
    ctx.stroke();
  }
}

Результат этого ниже:

Если вы захотите увидеть соединение линии, то можете удалить вызов moveTo().

Примечание: Подробнее о функции arc(),посмотрите Дуги .

Линии

Для рисования прямых линий используйте метод lineTo().

lineTo(x, y): Рисует линию с текущей позиции до позиции, определённой x и y.

Этот метод принимает два аргумента x и y, которые являются координатами конечной точки линии. Начальная точка зависит от ранее нарисованных путей, причём конечная точка предыдущего пути является начальной точкой следующего и т. д. Начальная точка также может быть изменена с помощью метода moveTo().

Пример ниже рисует два треугольника, один закрашенный и другой обведён контуром.

<html>
  <body onload="draw();">
    <canvas id="canvas" width="150" height="150"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    // Filled triangle
    ctx.beginPath();
    ctx.moveTo(25, 25);
    ctx.lineTo(105, 25);
    ctx.lineTo(25, 105);
    ctx.fill();

    // Stroked triangle
    ctx.beginPath();
    ctx.moveTo(125, 125);
    ctx.lineTo(125, 45);
    ctx.lineTo(45, 125);
    ctx.closePath();
    ctx.stroke();
  }
}

Отрисовка начинается с вызова beginPath(), чтобы начать рисовать путь новой фигуры. Затем мы используем метод moveTo(), чтобы переместить начальную точку в нужное положение. Ниже рисуются две линии, которые образуют две стороны треугольника.

Вы заметите разницу между закрашенным и обведённым контуром треугольниками. Это, как упоминалось выше, из-за того, что фигуры автоматически закрываются, когда путь заполнен (т. е. закрашен), но не тогда, когда он очерчен (т. е. обведён контуром). Если бы мы не учли closePath() для очерченного треугольника, тогда только две линии были бы нарисованы, а не весь треугольник.

Дуги

Для рисования дуг и окружностей, используем методы arc() и arcTo().

arc(x, y, radius, startAngle, endAngle, anticlockwise): Рисуем дугу с центром в точке (x,y) радиусом radius, начиная с угла startAngle и заканчивая в endAngle в направлении против часовой стрелки anticlockwise (по умолчанию по ходу движения часовой стрелки).
arcTo(x1, y1, x2, y2, radius): Рисуем дугу с заданными контрольными точками и радиусом, соединяя эти точки прямой линией.

Рассмотрим детальнее метод arc(), который имеет пять параметров: x и y — это координаты центра окружности, в которой должна быть нарисована дуга. radius — не требует пояснений. Углы startAngle и endAngle определяют начальную и конечную точки дуги в радианах вдоль кривой окружности. Отсчёт происходит от оси x. Параметр anticlockwise — логическое значение, которое, если true, то рисование дуги совершается против хода часовой стрелки; иначе рисование происходит по ходу часовой стрелки.

Примечание: Углы в функции arc() измеряют в радианах, не в градусах. Для перевода градусов в радианы вы можете использовать JavaScript-выражение: radians = (Math.PI/180)*degrees.

Следующий пример немного сложнее, чем мы рассматривали ранее. Здесь нарисованы 12 различных дуг с разными углами и заливками.

Два for цикла размещают дуги по столбцам и строкам. Для каждой дуги, мы начинаем новый контур, вызывая beginPath(). В этом коде каждый параметр дуги для большей ясности задан в виде переменной, но вам не обязательно делать так в реальных проектах.

Координаты x и y должны быть достаточно ясны. radius and startAngle — фиксированы. endAngle начинается со 180 градусов (полуокружность) в первой колонке и, увеличиваясь с шагом 90 градусов, достигает кульминации полноценной окружностью в последнем столбце.

Установка параметра clockwise определяет результат; в первой и третьей строках рисование дуг происходит по часовой стрелке, а во второй и четвёртой - против часовой стрелки. Благодаря if-условию верхняя половина дуг образуется с контуром, (обводкой), а нижняя половина дуг - с заливкой.

Примечание: Этот пример требует немного большего холста (canvas), чем другие на этой странице: 150 x 200 pixels.

<html>
  <body onload="draw();">
    <canvas id="canvas" width="150" height="200"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    for (var i = 0; i < 4; i++) {
      for (var j = 0; j < 3; j++) {
        ctx.beginPath();
        var x = 25 + j * 50; // x coordinate
        var y = 25 + i * 50; // y coordinate
        var radius = 20; // Arc radius
        var startAngle = 0; // Starting point on circle
        var endAngle = Math.PI + (Math.PI * j) / 2; // End point on circle
        var anticlockwise = i % 2 == 0 ? false : true; // clockwise or anticlockwise

        ctx.arc(x, y, radius, startAngle, endAngle, anticlockwise);

        if (i > 1) {
          ctx.fill();
        } else {
          ctx.stroke();
        }
      }
    }
  }
}

Безье и квадратичные кривые

Следующим типом доступных контуров являются кривые Безье, и к тому же доступны в кубическом и квадратичном вариантах. Обычно они используются при рисовании сложных составных фигур.

quadraticCurveTo(cp1x, cp1y, x, y): Рисуется квадратичная кривая Безье с текущей позиции пера в конечную точку с координатами x и y, используя контрольную точку с координатами cp1x и cp1y.
bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y): Рисуется кубическая кривая Безье с текущей позиции пера в конечную точку с координатами x и y, используя две контрольные точки с координатами (cp1x, cp1y) и (cp2x, cp2y).

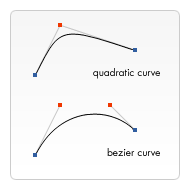Различие между ними можно увидеть на рисунке, изображённом справа. Квадратичная кривая Безье имеет стартовую и конечную точки (синие точки) и всего одну контрольную точку (красная точка), в то время как кубическая кривая Безье использует две контрольные точки.

Параметры x и y в этих двух методах являются координатами конечной точки. cp1x и cp1y — координаты первой контрольной точки, а cp2x и cp2y — координаты второй контрольной точки.

Использование квадратичных или кубических кривых Безье может быть спорным выходом, так как в отличие от приложений векторной графики типа Adobe Illustrator, мы не имеем полной видимой обратной связи с тем, что мы делаем. Этот факт делает довольно сложным процесс рисования сложных фигур. В следующем примере мы нарисуем совсем простую составную фигуру, но, если у вас есть время и ещё больше терпения, можно создать более сложные составные фигуры.

В этом примере нет ничего слишком тяжёлого. В обоих случаях мы видим последовательность кривых, рисуя которые, в результате получим составную фигуру.

Квадратичные кривые Безье

В этом примере многократно используются квадратичные кривые Безье для рисования речевой выноски.

<html>
  <body onload="draw();">
    <canvas id="canvas" width="150" height="150"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    // Quadratric curves example
    ctx.beginPath();
    ctx.moveTo(75, 25);
    ctx.quadraticCurveTo(25, 25, 25, 62.5);
    ctx.quadraticCurveTo(25, 100, 50, 100);
    ctx.quadraticCurveTo(50, 120, 30, 125);
    ctx.quadraticCurveTo(60, 120, 65, 100);
    ctx.quadraticCurveTo(125, 100, 125, 62.5);
    ctx.quadraticCurveTo(125, 25, 75, 25);
    ctx.stroke();
  }
}

Кубические кривые Безье

В этом примере нарисовано сердце с использованием кубических кривых Безье.

<html>
  <body onload="draw();">
    <canvas id="canvas" width="150" height="150"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    // Cubic curves example
    ctx.beginPath();
    ctx.moveTo(75, 40);
    ctx.bezierCurveTo(75, 37, 70, 25, 50, 25);
    ctx.bezierCurveTo(20, 25, 20, 62.5, 20, 62.5);
    ctx.bezierCurveTo(20, 80, 40, 102, 75, 120);
    ctx.bezierCurveTo(110, 102, 130, 80, 130, 62.5);
    ctx.bezierCurveTo(130, 62.5, 130, 25, 100, 25);
    ctx.bezierCurveTo(85, 25, 75, 37, 75, 40);
    ctx.fill();
  }
}

Прямоугольники

Все эти методы мы видели в Рисование прямоугольников, которые рисуют прямоугольники сразу в canvas, так же есть метод rect(), который не отображает, а только добавляет контур рисования (path) заданного прямоугольника к последнему открытому контуру.

rect(x, y, width, height): Добавляет в path прямоугольник, верхний левый угол которого указан с помощью (x, y) с вашими width и height

Когда этот метод вызван, автоматически вызывается метод moveTo() с параметрами (x, y). Другими словами, позиция курсора устанавливается в начало добавленного прямоугольника.

Создание комбинаций

До сих пор, в каждом примере использовался только один тип функции контуров для каждой фигуры. Однако, нет никаких ограничений на количество или типы контуров, которые вы можете использовать для создания фигур. Давайте в этом примере объединим все вышеперечисленные функции контуров, чтобы создать набор очень известных игровых персонажей.

<html>
  <body onload="draw();">
    <canvas id="canvas" width="150" height="150"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    roundedRect(ctx, 12, 12, 150, 150, 15);
    roundedRect(ctx, 19, 19, 150, 150, 9);
    roundedRect(ctx, 53, 53, 49, 33, 10);
    roundedRect(ctx, 53, 119, 49, 16, 6);
    roundedRect(ctx, 135, 53, 49, 33, 10);
    roundedRect(ctx, 135, 119, 25, 49, 10);

    ctx.beginPath();
    ctx.arc(37, 37, 13, Math.PI / 7, -Math.PI / 7, false);
    ctx.lineTo(31, 37);
    ctx.fill();

    for (var i = 0; i < 8; i++) {
      ctx.fillRect(51 + i * 16, 35, 4, 4);
    }

    for (i = 0; i < 6; i++) {
      ctx.fillRect(115, 51 + i * 16, 4, 4);
    }

    for (i = 0; i < 8; i++) {
      ctx.fillRect(51 + i * 16, 99, 4, 4);
    }

    ctx.beginPath();
    ctx.moveTo(83, 116);
    ctx.lineTo(83, 102);
    ctx.bezierCurveTo(83, 94, 89, 88, 97, 88);
    ctx.bezierCurveTo(105, 88, 111, 94, 111, 102);
    ctx.lineTo(111, 116);
    ctx.lineTo(106.333, 111.333);
    ctx.lineTo(101.666, 116);
    ctx.lineTo(97, 111.333);
    ctx.lineTo(92.333, 116);
    ctx.lineTo(87.666, 111.333);
    ctx.lineTo(83, 116);
    ctx.fill();

    ctx.fillStyle = "white";
    ctx.beginPath();
    ctx.moveTo(91, 96);
    ctx.bezierCurveTo(88, 96, 87, 99, 87, 101);
    ctx.bezierCurveTo(87, 103, 88, 106, 91, 106);
    ctx.bezierCurveTo(94, 106, 95, 103, 95, 101);
    ctx.bezierCurveTo(95, 99, 94, 96, 91, 96);
    ctx.moveTo(103, 96);
    ctx.bezierCurveTo(100, 96, 99, 99, 99, 101);
    ctx.bezierCurveTo(99, 103, 100, 106, 103, 106);
    ctx.bezierCurveTo(106, 106, 107, 103, 107, 101);
    ctx.bezierCurveTo(107, 99, 106, 96, 103, 96);
    ctx.fill();

    ctx.fillStyle = "black";
    ctx.beginPath();
    ctx.arc(101, 102, 2, 0, Math.PI * 2, true);
    ctx.fill();

    ctx.beginPath();
    ctx.arc(89, 102, 2, 0, Math.PI * 2, true);
    ctx.fill();
  }
}

// A utility function to draw a rectangle with rounded corners.

function roundedRect(ctx, x, y, width, height, radius) {
  ctx.beginPath();
  ctx.moveTo(x, y + radius);
  ctx.arcTo(x, y + height, x + radius, y + height, radius);
  ctx.arcTo(x + width, y + height, x + width, y + height - radius, radius);
  ctx.arcTo(x + width, y, x + width - radius, y, radius);
  ctx.arcTo(x, y, x, y + radius, radius);
  ctx.stroke();
}

Конечное изображение выглядит так:

Мы не будем подробно останавливаться на том, так как это на самом деле удивительно просто. Наиболее важные вещи, которые следует отметить, это использование свойства fillStyle в контексте рисования и использование функции утилиты (в данном случае roundedRect()). Использование функций утилиты для битов чертежа часто может быть очень полезным и сократить количество необходимого кода, а также его сложность.

Позже, в этом уроке, мы ещё раз рассмотрим fillStyle, но более подробно. Здесь же мы используем его для изменения цвета заливки путей вместо цвета по умолчанию от чёрного до белого, а затем обратно.

Path2D объекты

Как мы видели в последнем примере, есть серия путей и команд для рисования объектов на вашем холсте. Чтобы упростить код и повысить производительность, объект Path2D, доступный в последних версиях браузеров, позволяет вам кешировать или записывать эти команды рисования. Вы можете быстро запускать свои пути. Давайте посмотрим, как мы можем построить объект Path2D :

Path2D(): Конструктор Path2D() возвращает вновь созданный объект Path2D необязательно с другим путём в качестве аргумента (создаёт копию) или необязательно со строкой, состоящей из данных пути SVG path .

new Path2D(); // пустой path объект
new Path2D(path); // копирование из другого path
new Path2D(d); // path из SVG

Все методы path , такие как moveTo, rect, arc, или quadraticCurveTo, и т.п, которые мы уже знаем, доступны для объектов Path2D

API Path2D также добавляет способ комбинирования путей с использованием метода addPath. Это может быть полезно, если вы хотите, например, создавать объекты из нескольких компонентов.

Path2D.addPath(path [, transform]): Добавляет путь к текущему пути с необязательной матрицей преобразования.

Path2D пример

В этом примере мы создаём прямоугольник и круг. Оба они сохраняются как объект Path2D, поэтому они доступны для последующего использования. С новым API Path2D несколько методов были обновлены, чтобы при необходимости принять объект Path2D для использования вместо текущего пути. Здесь stroke и fill используются с аргументом пути, например, для рисования обоих объектов на холст.

<html>
  <body onload="draw();">
    <canvas id="canvas" width="130" height="100"></canvas>
  </body>
</html>

function draw() {
  var canvas = document.getElementById("canvas");
  if (canvas.getContext) {
    var ctx = canvas.getContext("2d");

    var rectangle = new Path2D();
    rectangle.rect(10, 10, 50, 50);

    var circle = new Path2D();
    circle.moveTo(125, 35);
    circle.arc(100, 35, 25, 0, 2 * Math.PI);

    ctx.stroke(rectangle);
    ctx.fill(circle);
  }
}

Использование SVG путей

Ещё одна мощная функция нового Canvas Path2D API использует данные пути SVG, SVG path data, для инициализации путей на вашем холсте. Это может позволить вам передавать данные пути и повторно использовать их как в SVG, так и в холсте.

Путь перемещается в точку (M10 10), а затем горизонтально перемещается на 80 пунктов вправо (h 80), затем на 80 пунктов вниз (v 80), затем на 80 пунктов влево (h -80), а затем обратно на start (z). Этот пример можно увидеть на странице Path2D constructor.

var p = new Path2D("M10 10 h 80 v 80 h -80 Z");