Blickpunkte und Betrachter: Kamerasimulation in WebXR
Das Erste und Wichtigste, das man verstehen muss, wenn man den Code zur Verwaltung von Sichtpunkten und Kameras in Ihrer Anwendung berücksichtigt, ist Folgendes: WebXR hat keine Kameras. Es gibt kein magisches Objekt, das entweder von der WebGL oder der WebXR API bereitgestellt wird, das den Betrachter darstellt, den Sie drehen und verschieben können, um automatisch zu ändern, was auf dem Bildschirm zu sehen ist. In diesem Leitfaden zeigen wir, wie man WebGL verwendet, um Kamera-Bewegungen zu simulieren, ohne eine Kamera bewegen zu müssen. Diese Techniken können in jedem WebGL- (oder WebXR-)Projekt verwendet werden.
Die Animation von 3D-Grafiken ist ein Bereich der Softwareentwicklung, der mehrere Disziplinen der Informatik, Mathematik, Kunst, Grafikdesign, Kinematik, Anatomie, Physiologie, Physik und Kinematografie vereint. Da wir keine echte Kamera haben, stellen wir uns eine vor und reproduzieren den Effekt einer Kamera, ohne tatsächlich die Fähigkeit zu haben, den Benutzer durch die Szene zu bewegen.
Es gibt einige Artikel zu den grundlegenden mathematischen, geometrischen und anderen Konzepten hinter WebGL und WebXR, die möglicherweise nützlich sind, bevor oder während Sie diesen hier lesen, darunter:
- Erklärung der grundlegenden 3D-Theorie
- Matrixmathematik für das Web
- WebGL-Modell-Ansicht-Projektion
- Geometrie und Referenzräume in WebXR
Notiz des Herausgebers: Die meisten Diagramme, die in diesem Artikel verwendet werden, um zu zeigen, wie sich die Kamera bei standardmäßigen Bewegungen bewegt, wurden einem Artikel auf der FilmmakerIQ-Website entnommen, nämlich von diesem Bild, das im ganzen Internet zu finden ist. Wir gehen aufgrund ihrer häufigen Wiederverwendung davon aus, dass sie unter einer zulässigen Lizenz verfügbar sind, der Eigentümer jedoch unsicher ist. Wir hoffen, dass es frei verwendbar ist; wenn nicht und Sie der Eigentümer sind, lassen Sie es uns bitte wissen und wir werden neue Diagramme finden oder erstellen. Oder wenn Sie damit einverstanden sind, dass wir die Bilder weiterhin verwenden, lassen Sie es uns bitte wissen, damit wir Ihnen ordnungsgemäß Anerkennung zollen können!
Kameras und relative Bewegung
Wenn ein klassischer Live-Action-Film gedreht wird, befinden sich die Schauspieler auf einem Set und bewegen sich darauf, während sie auftreten, wobei eine oder mehrere Kameras ihre Bewegungen beobachten. Die Kameras können an Ort und Stelle befestigt sein, können aber auch so eingerichtet sein, dass sie sich ebenfalls bewegen und so die Bewegungen der Darsteller verfolgen, sich hinein- und herauszoomen, um emotionale Wirkung zu erzielen und so weiter.
Virtuelle Kameras
In WebGL (und in der Erweiterung, in WebXR) gibt es kein Kameraobjekt, das wir bewegen und drehen können, also müssen wir einen Weg finden, diese Bewegungen zu imitieren. Da es keine Kamera gibt, müssen wir einen Weg finden, sie zu imitieren. Glücklicherweise haben uns Physiker wie Galileo, Newton, Lorentz und Einstein das Relativitätsprinzip gegeben, das besagt, dass die Gesetze der Physik in jedem Bezugssystem die gleiche Form haben. Das heißt, egal wo Sie stehen, die Gesetze der Physik wirken auf die gleiche Weise.
Wenn Sie und eine andere Person beispielsweise in einem leeren Feld aus soliden Stein stehen, mit nichts anderem als so weit das Auge reicht, und Sie sich drei Meter auf die andere Person zubewegen, sieht das Ergebnis gleich aus, als ob die andere Person sich drei Meter auf Sie zubewegt hätte. Es gibt keine Möglichkeit für einen von Ihnen, den Unterschied zu erkennen. Eine dritte Partei kann den Unterschied erkennen, aber die beiden von Ihnen nicht. Wenn Sie eine Kamera sind, können Sie das gleiche visuelle Ergebnis erzielen, indem Sie entweder die Kamera bewegen oder alles um die Kamera herum bewegen.
Und das ist unsere Lösung. Da wir die Kamera nicht bewegen können, bewegen wir die Welt um sie herum. Unser Renderer muss wissen, wo wir uns die Kamera vorstellen, und dann die Position jedes sichtbaren Objekts ändern, um diese Position und Ausrichtung zu simulieren. So bezieht sich der Begriff Kamera in der WebGL- und WebXR-Programmierung auf ein Objekt, das die Position und Blickrichtung eines hypothetischen Betrachters der Szene beschreibt, unabhängig davon, ob ein tatsächliches Objekt im 3D-Raum vorhanden ist oder nicht.
Blickpunkte
Da die Kamera ein virtuelles Objekt ist, das anstelle eines physischen Objekts in der virtuellen Welt die Position und Blickrichtung eines Betrachters darstellt, ist es nützlich, über die Arten von Situationen nachzudenken, die den Einsatz einer Kamera erfordern. Spielebezogene Situationen sind separat aufgeführt, da sie oft ein spezieller Fall sind, der für Spiele spezifisch ist, aber jede dieser Perspektiven könnte auf jede 3D-Grafikszene zutreffen.
Generalisierte Kameras
Im Allgemeinen können virtuelle Kameras in physische Objekte innerhalb der Szene integriert sein oder auch nicht. Tatsächlich ist es außerhalb des Bereichs der 3D-Spiele viel wahrscheinlicher, dass die Kamera nicht mit einem Objekt übereinstimmt, das überhaupt in der Szene erscheint. Einige Beispiele, wie 3D-Kameras verwendet werden:
- Beim Rendern von Animationen – sei es für die Filmproduktion oder für den Einsatz im Kontext einer Präsentation oder eines Spiels – wird die virtuelle Kamera genauso verwendet wie eine Filmkamera in der realen Welt. Soweit möglich, werden standardmäßige Kinematografie-Techniken verwendet, da der Betrachter wahrscheinlich mit Filmen aufgewachsen ist, die diese Techniken verwenden, und unbewusste Erwartungen hat, dass ein Film oder eine Animation diesen Methoden folgt. Abweichungen davon können den Betrachter aus dem Moment herausreißen.
- In Geschäftsanwendungen wird die 3D-Kamera verwendet, um die scheinbare Größe und Perspektive zu bestimmen, wenn Dinge wie Grafiken und Diagramme gerendert werden.
- In Kartenanwendungen kann die Kamera entweder direkt über der Szene platziert oder verschiedene Winkel verwendet werden, um Perspektive zu zeigen. Für 3D-GPS-Lösungen ist die Kamera so positioniert, dass der Bereich um den Benutzer herum gezeigt wird, wobei der Großteil der Anzeige den Bereich vor dem Bewegungspfad des Benutzers zeigt.
- Bei der Verwendung von WebGL zur Beschleunigung des Zeichnens von 2D-Grafiken wird die Kamera normalerweise direkt über der Mitte der Szene mit der Entfernung und dem Sichtfeld platziert, um die gesamte Szene darzustellen.
- Beim Beschleunigen von Bitmap-Grafiken würde der Renderer das 2D-Bild in einen WebGL-Texturpuffer zeichnen und dann die Textur neu zeichnen, um den Bildschirm zu aktualisieren. Dabei wird die Textur im Wesentlichen als Backbuffer zur Durchführung von Mehrfachpufferung in Ihrer 2D-Grafikanwendung verwendet.
Kameras im Gaming
Es gibt viele Arten von Spielen und dementsprechend gibt es mehrere Möglichkeiten, wie Kameras in Spielen eingesetzt werden können. Einige häufige Situationen umfassen:
- In einem First-Person-Spiel befindet sich die Kamera innerhalb des Kopfes des Avatars des Spielers und zeigt in die gleiche Richtung wie die Augen des Avatars. Auf diese Weise ist die Ansicht, die auf dem Bildschirm oder Headset des Spielers präsentiert wird, das, was sein Avatar sehen würde.
- In einigen Third-Person-Spielen befindet sich die Kamera in kurzer Entfernung hinter dem Avatar oder Fahrzeug des Spielers und zeigt sie von hinten, während sie sich durch die Spielwelt bewegen. Dies wird in vielen Mehrspieler-Online-Rollenspielen, bestimmten Shooter-Spielen und so weiter verwendet. Beliebte Beispiele sind World of Warcraft, Tomb Raider und Fortnite. Diese Kategorie umfasst auch Spiele, bei denen die Kamera direkt über der Schulter des Spielers platziert ist.
- Einige 3D-Spiele bieten die Möglichkeit, Ihren Blickwinkel zu ändern, z. B. um aus den verschiedenen Fenstern eines Flugzeugs in einem Flugsimulator zu schauen oder um die Ansichten von allen Überwachungskameras innerhalb des Spielniveaus zu sehen (ein gängiges Merkmal von Spionage- und Stealth-basierten Spielen). Diese Möglichkeit wird auch von Spielen mit Waffen mit Zielfernrohren genutzt, bei denen die Ansicht nicht mehr ganz auf der Position des Kopfes basiert.
- 3D-Spiele könnten auch die Möglichkeit bieten, dass Nicht-Spieler die Aktion beobachten können, entweder indem sie einen unsichtbaren Avatar positionieren oder indem sie eine feste virtuelle Kamera auswählen, von der aus sie zuschauen können.
- In fortgeschrittenen 3D-Spielen könnte ein Kamera- oder Kamera-ähnliches Objekt verwendet werden, um zu bestimmen, was ein Nicht-Spieler-Charakter sehen kann, und dabei die gleiche Rendering- und Physik-Engine wie bei Spielercharakteren zu verwenden.
- In Einzelbildschirm-2D-Spielen ist die Kamera nicht direkt mit dem Spieler oder einem anderen Charakter im Spiel verbunden, sondern sie ist entweder fixiert über oder neben dem Spielfeldbereich oder folgt der Aktion, während sich die Aktion in einer scrollenden Spielwelt bewegt. Zum Beispiel findet ein klassisches Arcade-Spiel wie Pac-Man auf einer festen Spielkarte statt, sodass die Kamera in einer festen Entfernung über der Karte bleibt und immer direkt auf die Spielwelt gerichtet ist.
- In einem seitlich oder oben scrollenden Spiel wie Super Mario Bros. bewegt sich die Kamera nach links und rechts (oder auf und ab oder beides), um sicherzustellen, dass die Aktion sichtbar bleibt, auch wenn das Spiellevel viel größer ist als das Sichtfenster.
Positionierung der Kamera
Da es in WebGL oder WebXR keine Standard-Kameraobjekte gibt, müssen wir die Kamera selbst simulieren. Bevor wir dies tun können, und bevor wir dann die Bewegung der Kamera simulieren können, betrachten wir zunächst die virtuelle Kamera und wie sie sich auf die grundlegendste Ebene bewegen kann. Wie bei allen Dingen kann die Position eines Objekts im Raum – auch wenn dieser Raum virtuell ist – durch drei Zahlen dargestellt werden, die seine Position relativ zum Ursprung angeben, dessen Position als (0, 0, 0) definiert ist.
Es gibt einen weiteren Aspekt der räumlichen Beziehung eines Objekts zum Ursprung im Raum, der berücksichtigt werden muss: Perspektive. Perspektive, die auf die Objekte in einer Szene ordnungsgemäß angewendet wird, kann eine Szene, die sonst so flach wie ein typischer 2D-Bildschirm erscheinen würde, zum Leben erwecken, als wäre sie wirklich 3D. Es gibt mehrere Arten von Perspektiven; diese sind definiert und ihre Mathematik ist im Artikel WebGL-Modell-Ansicht-Projektion erklärt. Wichtig ist, dass die Wirkung der Perspektive auf einen Vektor durch Hinzufügen einer vierten Komponente zum Vektor dargestellt werden kann: die Perspektivenkomponente, genannt w.
Der Wert von w wird angewendet, indem jede der anderen drei Komponenten durch ihn geteilt wird, um die endgültige Position oder den endgültigen Vektor zu erhalten; das heißt, für eine als (x, y, z, w) angegebene Koordinate ist der Punkt im 3D-Raum tatsächlich (x/w, y/w, z/w, 1) oder (x/w, y/w, z/w). Wenn Sie keine Perspektive verwenden, ist w immer 1. In dieser Situation lauten die vollständigen Koordinaten für ein Objekt, das sich bei (1, 0, 3) befindet, (1, 0, 3, 1).
Aber die Lage ist nicht ausreichend, um ein Objekt im 3D-Raum zu beschreiben, denn der Zustand eines Objekts im Raum bezieht sich nicht nur auf seine Lage, sondern auch auf seine Drehung oder Blickrichtung, auch bekannt als seine Orientierung. Die Orientierung kann durch einen 3D-Vektor dargestellt werden, der typischerweise normalisiert wird, sodass seine Länge 1,0 beträgt. Zum Beispiel, wenn das Objekt auf ein Objekt blickt, das sich bei (3, 1, -2) befindet – das heißt, drei Meter nach rechts, ein Meter nach oben und zwei Meter vom Ursprungspunkt entfernt – ist das Ergebnis:
Dies kann auch als ein Array dargestellt werden:
let directionVector = [3, 1, -2];
Für die Zwecke von Operationen, die sowohl die Koordinaten als auch den Blickrichtungsvektor betreffen, muss der Vektor die w-Komponente enthalten. Der Wert von w ist für Vektoren immer 0, sodass der vorhergehende Vektor auch unter Verwendung von [3, 1, -2, 0] oder:
WebXR normalisiert Vektoren automatisch so, dass sie eine Länge von 1 Meter haben; jedoch kann es sinnvoll sein, es selbst durchzuführen, aus verschiedenen Gründen, wie zum Beispiel um die Leistung der Berechnungen zu verbessern, indem man die Normalisierung nicht wiederholt durchführen muss.
Sobald Sie die Matrix bestimmt haben, die die gewünschten Kamera-Bewegungen darstellt, müssen Sie sie umkehren, da Sie die Kamera nicht bewegen. Da Sie tatsächlich alles außer der Kamera bewegen, nehmen Sie die Inverse der Transformationsmatrix, um eine inverse Transformationsmatrix zu erhalten. Diese inverse Matrix kann dann auf die Objekte in der Welt angewendet werden, um deren Positionen und Ausrichtungen zu ändern, um die gewünschte Kameraposition zu simulieren.
Aus diesem Grund verfügt das von WebXR verwendete XRRigidTransform-Objekt, um Transformationen darzustellen, über eine inverse-Eigenschaft. Die inverse-Eigenschaft ist ein weiteres XRRigidTransform-Objekt, das die Inverse der übergeordneten Transformation ist. Da die XRView, die die Ansicht darstellt, eine transform-Eigenschaft hat, die ein XRRigidTransform bereitstellt, können Sie die Modellansichtsmatrix—die Transformationsmatrix, die benötigt wird, um die Welt zu bewegen, um die gewünschte Kameraposition zu simulieren—so erhalten:
let viewMatrix = view.transform.inverse.matrix;
Wenn die von Ihnen verwendete Bibliothek ein XRRigidTransform-Objekt direkt akzeptiert, können Sie stattdessen view.transform.inverse erhalten, anstatt nur das Array zu übernehmen, das die Ansichts-Matrix darstellt.
Zusammensetzen von mehreren Transformationen
Wenn Ihre Kamera gleichzeitig mehrere Transformationen ausführen muss, wie z. B. Zoomen und Schwenken gleichzeitig, können Sie die Transformations-Matrizen miteinander multiplizieren, um sie in eine einzige Matrix zu kombinieren, die beide Änderungen auf einmal anwendet. Siehe Multiplikation von zwei Matrizen im Artikel Matrixmathematik für das Web für eine klare, aber lesbare Funktion, die dies durchführt, oder verwenden Sie Ihre bevorzugte Matrix-Mathematikbibliothek wie glMatrix, um die Arbeit zu erledigen.
Es ist wichtig, sich daran zu erinnern, dass im Gegensatz zur typischen Arithmetik, bei der die Multiplikation kommutativ ist (das heißt, Sie erhalten das gleiche Ergebnis, egal ob Sie von links nach rechts oder von rechts nach links multiplizieren), die Matrix-Multiplikation nicht kommutativ ist! Dies liegt daran, dass jede Transformation die Position des Objekts und möglicherweise das Koordinatensystem selbst beeinflusst, was die Ergebnisse der nächsten durchgeführten Operation drastisch ändern kann. Daher müssen Sie vorsichtig sein, in welcher Reihenfolge Sie Ihre Transformationen anwenden, wenn Sie ihre zusammengesetzte Transformation erstellen (oder Transformationen direkt in Folge anwenden).
Anwenden der Transformation
Um die Transformation anzuwenden, multiplizieren Sie den Punkt oder Vektor mit der Transformation oder der Zusammensetzung der Transformationen.
Dies war ein sehr schneller Überblick über die Konzepte der Position in Bezug auf den physischen Ort, die Orientierung oder Blickrichtung und die Perspektive. Weitere Details zu diesem Thema finden Sie in den Artikeln Geometrie und Referenzräume, WebGL-Modell-Ansicht-Projektion und Matrixmathematik für das Web.
Klassische Kinematografie simulieren
Kinematografie ist die Kunst, Kamerabewegungen zu entwerfen, zu planen und auszuführen, um das gewünschte Aussehen und die gewünschte Emotion für eine Szene in Animation oder Film zu schaffen. Es gibt eine Reihe von Begriffen, die hilfreich zu verstehen sind, hauptsächlich in Bezug auf Kamerabewegungen, da diese Begriffe verwendet werden, um entworfene Blickpunktänderungen mit der virtuellen Kamera zu beschreiben. Es ist auch völlig möglich, mehr als eine dieser Bewegungen gleichzeitig auszuführen; zum Beispiel können Sie die Kamera schwenken, während Sie gleichzeitig in die Szene hineinzoomen.
Denken Sie daran, dass die meisten Kamerabewegungen relativ zum Referenzraum der Kamera beschrieben werden.
Das Format zur Speicherung von Matrizen ist allgemein als flaches Array in Spalten-Major-Ordnung; das heißt, die Werte aus der Matrix werden beginnend mit der oberen linken Ecke und dann nach unten bis zur unteren Ecke bewegt, dann in die rechte Reihe übergegangen und wiederholt, bis alle Werte im Array sind.
Also eine Matrix, die so aussieht:
Wird in Array-Form so dargestellt:
let matrixArray = [
a1, a2, a3, a4,
a5, a6, a7, a8,
a9, a10, a11, a12,
a13, a14, a15, a16,
];
In diesem Array enthält die linkeste Spalte die Einträge a1, a2, a3, und a4. Die oberste Reihe enthält die Einträge a1, a5, a9, und a13.
Denken Sie daran, dass die meiste WebGL- und WebXR-Programmierung mit Drittanbieterbibliotheken durchgeführt wird, die auf der Grundfunktionalität von WebGL aufbauen, indem sie Routinen hinzufügen, die es viel einfacher machen, nicht nur grundlegende Matrix- und andere Operationen durchzuführen, sondern oft auch diese Standard-Kinematografie-Techniken zu simulieren. Sie sollten ernsthaft in Erwägung ziehen, eine davon zu verwenden, anstatt WebGL direkt zu verwenden. Dieser Leitfaden verwendet WebGL direkt, da es nützlich ist, zu einem gewissen Grad zu verstehen, was unter der Haube vor sich geht, und bei der Entwicklung von Bibliotheken zu helfen oder Ihnen zu helfen, den Code zu optimieren.
Hinweis: Auch wenn wir Phrasen wie "die Kamera bewegen" verwenden, bewegen wir in Wirklichkeit die gesamte Welt um die Kamera herum. Dies beeinflusst die Funktionsweise bestimmter Werte, worauf weiter unten hingewiesen wird.
Zoomen
Einer der bekanntesten Kameraeffekte ist der Zoom. Zoomen wird in einer physischen Kamera durch Ändern der Brennweite des Objektivs durchgeführt; dies ist der Abstand zwischen der Mitte des Objektivs selbst und den Lichtsensoren der Kamera. Somit ist Zoomen tatsächlich nicht mit einer physischen Bewegung der Kamera verbunden. Stattdessen verändert ein Zoom die Vergrößerung der Kamera über Zeit, um den Fokusbereich näher oder weiter weg vom Betrachter erscheinen zu lassen, ohne tatsächlich physisch die Kamera zu bewegen. Eine langsame Bewegung kann einer Szene Bewegung, Leichtigkeit oder Fokus verleihen, während ein schneller Zoom ein Gefühl von Angst, Überraschung oder Spannung erzeugen kann.
Da ein Zoom nicht die Position der Kamera bewegt, wirkt der resultierende Effekt unnatürlich. Das menschliche Auge hat kein Zoomobjektiv. Wir machen Dinge kleiner oder größer, indem wir uns von ihnen entfernen oder nähern. In der Kinematografie wird dies eine dolly shot genannt.
Es gibt zwei Techniken in 3D-Grafiken, die ähnliche, aber nicht identische Ergebnisse erzeugen können, und deren Methoden sich in verschiedenen Situationen leichter anwenden lassen.
Zoomen durch Anpassung des Sichtfelds
Sie können etwas Nähers an einem echten "Zoom" tun, indem Sie das Sichtfeld (FOV) der Kamera ändern. Das Sichtfeld ist ein Winkel, der die Länge des Bogens auf dem gesamten sichtbaren Bereich rund um die Kamera definiert, der gleichzeitig sichtbar sein soll. Dies ist eine Wirkung der Brennweite in einer physischen Kamera, sodass, da es keine echte Kamera gibt, die Änderung des FOV ein akzeptabler Ersatz ist.
Erinnern Sie sich daran, dass der Umfang eines Kreises 2π⋅r Radiant (360°) beträgt; dies ist daher das theoretische maximale FOV. Realistisch gesehen sehen Menschen jedoch nicht annähernd so viel und Anzeigegeräte wie Monitore und VR-Brillen tendieren dazu, das Sichtfeld noch weiter zu reduzieren. Menschliche Augen haben typischerweise ein horizontales Sichtfeld von etwa 135° (ca. 2,356 Radiant) und ein vertikales FOV von etwa 180° (π oder ca. 3,142 Radiant).
Das Verkleinern des FOV der Kamera reduziert den Bogen, der im Sichtfenster enthalten ist, und vergrößert so diesen Inhalt, wenn er im Sichtfenster gerendert wird. Es gibt Unterschiede zwischen diesem und einem optischen Zoomeffekt, aber das Ergebnis ist im Allgemeinen nah genug, um die Arbeit zu erledigen.
Die folgende Funktion gibt eine Projektionsperspektivmatrix zurück, die den angegebenen Sichtfeldwinkel sowie die festgelegten Nah- und Fern-Ebenenentfernungen integriert:
function createPerspectiveMatrix(viewport, fovDegrees, nearClip, farClip) {
const fovRadians = fovDegrees * (Math.PI / 180.0);
const aspectRatio = viewport.width / viewport.height;
const transform = mat4.create();
mat4.perspective(transform, fovRadians, aspectRatio, nearClip, farClip);
return transform;
}
Nach der Umwandlung des FOV-Winkels, fovDegrees, von Grad in Radianten und der Berechnung der Bildformatverhältnisses des XRViewport, das durch den viewport-Parameter angegeben wird, verwendet diese Funktion die mat4.perspective()-Funktion der glMatrix-Bibliothek, um die Perspektivmatrix zu berechnen.
Die Perspektivmatrix umfasst den Sichtfeld (technisch handelt es sich um den vertikalen Sichtfeld), das Bildformatverhältnis und die nahe und ferne Clipping-Ebene innerhalb der 4x4-Matrix transform, die dann an den Aufrufer zurückgegeben wird.
Die nahe Clipping-Ebene ist der Abstand in Metern zu einer Ebene parallel zur Anzeigefläche, näher als die nichts gezeichnet wird. Verzeichnisse, die sich auf der gleichen Seite dieser Ebene wie die Kamera befinden, werden nicht gezeichnet. Im Gegensatz dazu ist die ferne Clipping-Ebene der Abstand in Metern zu einer Ebene, jenseits derer keine Verzeichnisse gezeichnet werden.
Um mit einem Skalierungsfaktor oder Prozentsatz zu zoomen, können Sie 1x (100% der normalen Größe) auf den größten FOV-Wert abbilden, den Sie zulassen (was dazu führt, dass der größte Inhalt sichtbar ist), dann Ihre maximale Vergrößerung auf den maximalen FOV-Wert, den Sie unterstützen, und entsprechende Werte dazwischen abbilden.
Wenn Sie jeder Frame-Rendering-Durchlauf mit der Berechnung der Perspektivmatrix beginnen, können Sie in diese Matrix alle anderen Transformationen multiplizieren, die angewendet werden müssen, um die gewünschte Geometrie des Frames zu erhalten. Zum Beispiel:
const transform = createPerspectiveMatrix(viewport, 130, 1, 100);
const translateVec = vec3.fromValues(
-trackDistance,
-craneDistance,
pushDistance,
);
mat4.translate(transform, transform, translateVec);
Dies beginnt mit der Perspektivmatrix, die ein 130° vertikales Sichtfeld darstellt, und wendet dann eine Übersetzung an, die die Kamera so bewegt, dass sie verfolgen, kranen und drücken Bewegungen einschließt.
Skalierungstransformationen
Im Gegensatz zu einem echten "Zoom" beinhaltet Skalierung die Multiplikation jedes x, y und z Koordinatenwertes einer Position oder eines Verzeichnisses mit einem Skalierungsfaktor für diese Achse. Diese müssen nicht unbedingt für jede Achse identisch sein, obwohl das dem Zoom-Effekt am nächsten kommende Ergebnis darin beteiligt wäre, denselben Wert für jede zu verwenden. Dies müsste auf jeder Verzeichnis in der Szene angewendet werden – idealerweise im Vertex-Shader.
Wenn Sie um einen Faktor von 2 skalieren möchten, müssen Sie jede Komponente mit 2,0 multiplizieren. Um um den gleichen Betrag zu verkleinern, multiplizieren Sie sie mit -2,0. In Matrixbegriffen wird dies unter Verwendung einer Transformationsmatrix mit Skalierung durchgeführt, wie hier:
let scaleTransform = [
Sx, 0, 0, 0,
0, Sy, 0, 0,
0, 0, Sz, 0,
0, 0, 0, 1
];
Diese Matrix stellt eine Transformation dar, die um einen Faktor skaliert wird, der durch (Sx, Sy, Sz) angezeigt wird, wobei Sx den Skalierungsfaktor entlang der X-Achse, Sy den Skalierungsfaktor entlang der Y-Achse darstellt, und Sz den Faktor für die Z-Achse. Wenn einer dieser Werte von den anderen abweicht, wird das Ergebnis eine Dehnung oder Kontraktion sein, die in einigen Dimensionen im Vergleich zu anderen unterschiedlich ist.
Wenn der gleiche Skalierungsfaktor in jede Richtung angewendet werden soll, können Sie eine einfache Funktion erstellen, um die Skalierungstransformationsmatrix für Sie zu generieren:
function createScalingMatrix(f) {
return [f, 0, 0, 0, 0, f, 0, 0, 0, 0, f, 0, 0, 0, 0, 1];
}
Mit der Transformationsmatrix in der Hand wenden wir die Transformation scaleTransform auf den Vektor (oder Verzeichnis) myVector an:
let myVector = [2, 1, -3];
let scaleTransform = [2, 0, 0, 0, 0, 2, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1];
vec4.transformMat4(myVector, myVector, scaleTransform);
Oder wir verwenden die Skalierung entlang jeder Achse mit dem selben Faktor unter Verwendung der oben gezeigten Funktion createScalingMatrix():
let myVector = [2, 1, -3];
vec4.transformMat4(myVector, myVector, createScalingMatrix(2.0));
Schwenken (nach links oder rechts neigen)
Schwenken oder Gier ist die Drehung der Kamera von links nach rechts oder vice versa, während ihr Basis ansonsten an Ort und Stelle fixiert ist. Die Position der Kamera im Raum ändert sich nicht, nur die Richtung, in die sie schaut. Und diese Richtung ändert sich nicht außer horizontal. Schwenken ist großartig für die Etablierung einer Einstellung oder das Bereitstellen eines Gefühls von Reichweite in einem weiten Raum oder an einem großen Objekt. Oder einfach zum Schauen nach links und rechts, wie die Simulation des Players, der seinen Kopf in einem immersiven oder VR-Szenario dreht.

Um dies zu tun, müssen wir um die Y-Achse rotieren, um die links- und rechtsdrehung der Kamera zu simulieren. Mit der glMatrix-Bibliothek, die wir zuvor verwendet haben, kann dies unter Verwendung der rotateY()-Methode für die mat4-Klasse durchgeführt werden, die eine Standard-4x4-Matrix darstellt. Um die Perspektive, die durch die Matrix viewMatrix definiert ist, um panAngle Radiant zu rotieren:
mat4.rotateY(viewMatrix, viewMatrix, panAngle);
Wenn panAngle positiv ist, schwenkt diese Transformation die Kamera nach rechts; ein negativer Wert für panAngle wird nach links schwenken.
Neigen (nach oben oder unten kippen)
Wenn Sie die Kamera neigen oder kippen, halten Sie sie im Raum an den gleichen Koordinaten fixiert, während Sie die vertikale Blickrichtung ändern, ohne den horizontalen Teil ihrer Blickrichtung zu verändern. Es passt die Richtung an, in der es nach oben oder unten zeigt. Neigen ist gut, um den Umfang eines hohen Objekts oder Szene zu erfassen, wie einen Wald oder einen Berg, ist aber auch eine beliebte Methode, um einen Charakter oder einen bedeutenden oder ehrfurchtgebietenden Ort vorzustellen. Es ist auch natürlich nützlich, um die Unterstützung für einen Spieler zu implementieren, der nach oben und unten schauen möchte.

Das Neigen der Kamera kann daher durch die Rotation der Kamera um die X-Achse erreicht werden, sodass sie sich dreht, um auf und ab zu schauen. Dies kann unter Verwendung der geeigneten Methode in Ihrer Matrix-Mathematikbibliothek durchgeführt werden, wie z. B. der rotateX()-Methode in glMatrixs mat4-Klasse:
mat4.rotateX(viewMatrix, viewMatrix, angle);
Positive Werte für angle neigen die Kamera nach unten, während negative Werte für angle nach oben neigen.
Dollying (vorwärts oder rückwärts bewegen)
Ein Dolly-Shot ist einer, bei dem die gesamte Kamera vorwärts und rückwärts bewegt wird. In der klassischen Filmproduktion wird dies typischerweise mit der Kamera auf einer Schiene oder auf einem sich bewegenden Fahrzeug montiert. Die resultierende Bewegung kann beeindruckend glatte Effekte erzeugen, insbesondere wenn sie sich mit der Person oder dem Objekt bewegt, das der Fokus Ihrer Aufnahme ist.

Obwohl ein Dolly-Shot und ein Zoom gleich aussehen sollten, tun sie das nicht. Die Tatsache, dass das Zoomen die Brennweite der Kamera verändert, bedeutet, dass sich die räumliche Beziehung zwischen dem Ziel und seiner Umgebung nicht ändert, obwohl das Ziel im Rahmen größer oder kleiner wird. Ein Dolly-Shot hingegen, indem er die Kamera tatsächlich bewegt, repliziert das Gefühl der physischen Bewegung und verursacht, dass sich die Beziehungen der Objekte in der Szene verändern, wie Sie es beim Vorbeigehen erwarten, während Sie auf das Ziel der Aufnahme zu- oder weggehen.
Um eine Dolly-Operation auszuführen, übersetzen Sie die Kameraansicht vorwärts und rückwärts entlang der Z-Achse:
mat4.translate(viewMatrix, viewMatrix, [0, 0, dollyDistance]);
Hier ist [0, 0, dollyDistance] ein Vektor, bei dem dollyDistance die Entfernung ist, die die Kamera dolly soll. Da dies durch das Bewegen der gesamten Welt um die Kamera funktioniert, bewegt sich die gesamte Welt relativ zur Kamera entlang der Z-Achse um dollyDistance Meter. Wenn dollyDistance positiv ist, bewegt sich die Welt in Richtung des Benutzers um diesen Betrag, was dazu führt, dass die Kamera näher an der Szene ist. Umgekehrt, negative Werte für dollyDistance bewegen die Welt vom Benutzer weg, wodurch die Kamera scheinbar vom Ziel zurückweicht.
Trucking (Nach links oder rechts bewegen)
Trucking unter Verwendung einer physischen Kamera verwendet dieselbe Art von Rigging wie beim Dollying, aber anstatt die Kamera vorwärts und rückwärts zu bewegen, bewegt sie sich von links nach rechts oder vice versa. Die Kamera dreht sich gar nicht, sodass der Fokus der Aufnahme langsam vom Bildschirm gleitet. Dies kann Konzentriertheit, Zeitverlauf oder Nachdenken vorschlagen, wenn versucht wird, eine Emotion in einer Szene zu etablieren. Es wird auch häufig in "Geh-und-Sprech"-Szenen verwendet, bei denen die Kamera gleitet neben den Charakteren und sie durch die Szene laufen.

Um die Kamera nach links und rechts zu bewegen, übersetzen Sie die Ansichts-Matrix entlang der X-Achse in die entgegengesetzte Richtung der gewünschten Kamerabewegung:
mat4.translate(viewMatrix, viewMatrix, [-truckDistance, 0, 0]);
Beachten Sie den Vektor [-truckDistance, 0, 0]. Dies kompensiert die Tatsache, dass die Truck-Operation durch Bewegen der Welt statt der Kamera funktioniert. Indem wir die ganze Welt in die entgegengesetzte Richtung von der durch truckDistance angegebenen Richtung bewegen, erreichen wir den Effekt, die Kamera in die erwartete Richtung zu bewegen. Auf diese Weise bewegen positive Werte von truckDistance die Kamera nach rechts (indem sie die Welt nach links bewegen) und negative Werte von truckDistance bewegen die Kamera nach links, indem sie die Welt nach rechts bewegen.
Pedestal (Hoch- und runter bewegen)
Ein Pedestal-Shot ist eine, bei der die Kamera in horizontaler Richtung relativ zum Boden fixiert ist, aber sich gerade auf und ab bewegt. Stellen Sie sich die Kamera auf einem Podest (oder Pfosten) vor, das größer oder kleiner wird. Dies ist nützlich, um ein Subjekt zu verfolgen, das größer oder kleiner wird, sich von einem Stuhl erhebt oder hinsetzt oder sich gerade nach oben und unten bewegt.

Ähnlich einem Kran-Aufnahme, die das Bewegen einer an einem Kran befestigten Kamera nach oben und unten beinhaltet. Um eine Podest- oder Kranbewegung auszuführen, übersetzen Sie die Ansicht entlang der Y-Achse in die entgegengesetzte Richtung der Richtung, in die Sie die Kamera bewegen möchten:
mat4.translate(viewMatrix, viewMatrix, [0, -pedestalDistance, 0]);
Indem Sie den Wert von pedestalDistance negieren, kompensieren Sie die Tatsache, dass Sie tatsächlich die Welt und nicht die Kamera bewegen. Auf diese Weise bewegen positive Werte von pedestalDistance die Kamera nach oben, während negative Werte sie nach unten bewegen.
Neigen (Links und rechts rollen)
Neigen (oder Rollen) ist eine Rotation der Kamera um ihre Rollachse; das heißt, die Kamera bleibt im Raum fixiert und bleibt auf denselben Punkt gerichtet, aber dreht sich um, sodass die Oberseite der Kamera in eine andere Richtung zeigt.
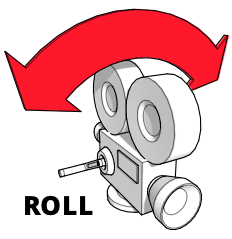
Sie können dies visualisieren, indem Sie Ihren Arm vor sich strecken und Ihre Hand offen halten, mit der Handfläche nach unten. Stellen Sie sich vor, dass Ihre Hand die Kamera ist und die Rückseite Ihrer Hand die Oberseite der Kamera darstellt. Drehen Sie nun Ihre Hand so, dass die "Kamera" kopfüber ist. Sie haben gerade Ihre Hand um die Rollachse geneigt. In der Kinematografie kann Neigung verwendet werden, um verschiedene Arten unsicherer Bewegungen wie Wellen oder Turbulenzen zu simulieren, kann aber auch dramatisch sein.
Um diese Rotation um die Z-Achse mit glMatrix durchzuführen:
mat4.rotateZ(viewMatrix, viewMatrix, cantAngle);
Bewegungen kombinieren
Sie können mehrere Bewegungen gleichzeitig ausführen, wie Zoomen beim Schwenken oder Neigen und Rollen zur gleichen Zeit.
Übersetzen entlang mehrerer Achsen
Das Übersetzen entlang mehrerer Achsen ist ziemlich einfach. Zuvor haben wir unsere Übersetzungen so ausgeführt:
mat4.translate(viewMatrix, viewMatrix, [-truckDistance, 0, 0]);
mat4.translate(viewMatrix, viewMatrix, [0, -pedestalDistance, 0]);
mat4.translate(viewMatrix, viewMatrix, [0, 0, dollyDistance]);
Die offensichtliche Lösung hier ist. Da die Übersetzung als Vektor ausgedrückt wird, der die Entfernung angibt, die entlang jeder Achse verschoben werden soll, können wir diese so kombinieren:
mat4.translate(viewMatrix, viewMatrix, [
-truckDistance,
-pedestalDistance,
dollyDistance,
]);
Dies wird den Ursprung der Matrix viewMatrix um den angegebenen Betrag entlang jeder Achse verschieben.
Rotieren um mehrere Achsen
Sie können auch Drehungen um mehrere Achsen zu einer einzigen Drehung um einen Quaternion, der eine gemeinsame Achse für die Drehungen darstellt, kombinieren. Um die Drehungen separat durchzuführen, verwenden Sie Euler-Winkel (separate Winkel um jede Achse) um einen Pitch, ein Gier und ein Roll wie folgt anzuwenden:
mat4.rotateX(viewMatrix, viewMatrix, pitchAngle);
mat4.rotateY(viewMatrix, viewMatrix, yawAngle);
mat4.rotateZ(viewMatrix, viewMatrix, rollAngle);
Sie können stattdessen einen Quaternion konstruieren, der eine kombinierte Drehachse aus den Euler-Winkeln darstellt, dann die Matrix mithilfe der Multiplikation rotieren, wie folgt:
const axisQuat = quat.create();
const rotateMatrix = mat4.create();
quat.fromEuler(axisQuat, pitchAngle, yawAngle, rollAngle);
mat4.fromQuat(rotateMatrix, axisQuat);
mat4.multiply(viewMatrix, viewMatrix, rotateMatrix);
Dies konvertiert die Euler-Winkel für Pitch, Gier und Roll in einen Quaternion, der alle drei Drehungen repräsentiert. Dies wird dann in eine Rotations-Transformationsmatrix konvertiert; anschließend wird die Ansichts-Matrix mit der Rotations-Transformation multipliziert, um die Drehungen abzuschließen.
Darstellung von 3D mit WebXR
WebXR geht einen Schritt weiter als 3D-Grafiken und ermöglicht deren Darstellung mithilfe spezieller visueller Hardware wie Brillen oder einem Headset, um 3D-Grafiken zu erzeugen, die scheinbar tatsächlich in drei Dimensionen existieren, möglicherweise im Kontext der realen Welt (im Falle der erweiterten Realität).
Um Tiefe wahrzunehmen, ist es notwendig, zwei Perspektiven auf die Szene zu haben. Durch den Vergleich der beiden Ansichten ist es möglich, die Tiefe der Objekte und in der Folge die Entfernung zwischen dem Betrachter und den gesehenen Objekten zu erkennen. Deshalb haben wir zwei Augen, die leicht auseinander liegen. Sie können sich daran erinnern, indem Sie ein Auge gleichzeitig schließen, zwischen den Augen wechseln. Beachten Sie, wie Ihr linkes Auge die linke Seite Ihrer Nase sehen kann, aber nicht die rechte, während Ihr rechtes Auge die rechte Seite Ihrer Nase sehen kann, aber nicht die linke. Das ist nur einer von vielen Unterschieden, die zwischen dem, was jedes Ihrer Augen sieht, existieren.
Unser Gehirn empfängt zwei Datensätze über Lichtpegel und Wellenlängen in unserem Sichtfeld – einer von jedem Auge. Das Gehirn verwendet diese Daten, um die Szene in unserem Geist zu konstruieren, wobei es die geringen Unterschiede zwischen den beiden Perspektiven verwendet, um Tiefe und Ent fernung zu ermitteln.
Rendering der Szene
Ein XR – eine Abkürzung, die sowohl Virtual Reality (VR) als auch Augmented Reality (AR) umfasst – Headset präsentiert uns 3D-Bilder, indem es zwei Ansichten der Szene zeichnet, die leicht versetzt voneinander sind, ähnlich den Ansichten, die durch unsere beiden Augen erhalten werden. Diese Ansichten werden dann separat jedem Auge zugeführt, um ihnen die Darstellung von Daten zu ermöglichen, die unser Gehirn benötigt, um ein 3D-Bild zu konstruieren.
Zu diesem Zweck fordert WebXR Ihren Renderer auf, die Szene zweimal für jedes einzelne Videobild zu zeichnen, einmal für jedes Auge. Die beiden Ansichten werden im selben Framepuffer gerendert, einmal links und einmal rechts. Das XR-Gerät verwendet dann Bildschirme und Linsen, um die linke Hälfte des erzeugten Bildes unserem linken Auge und die rechte Hälfte unserem rechten Auge zu präsentieren.
Zum Beispiel betrachten Sie ein Gerät, das einen Framepuffer mit 2560x1440 Pixeln verwendet. Die Aufteilung in zwei Teile – die eine Hälfte für jedes Auge – führt dazu, dass die Ansicht jedes Auges mit einer Auflösung von 1280x1440 Pixeln gezeichnet wird. Hier ist, wie das konzeptionell aussieht:
Ihr Code teilt der WebXR-Engine mit, dass Sie das nächste Animationsbild bereitstellen möchten, indem Sie die XRSession-Methode requestAnimationFrame() aufrufen und eine Rückruffunktion angeben, die ein Animationsbild rendert. Wenn der Browser Sie auffordert, die Szene zu rendern, ruft er die Rückruffunktion auf und übergibt als Eingabeparameter die aktuelle Zeit und ein XRFrame, das die benötigten Daten zum Rendern des korrekten Bildes kapselt.
Diese Informationen umfassen die XRViewerPose, die die Position und Blickrichtung des Betrachters innerhalb der Szene sowie eine Liste von XRView-Objekten beschreibt, von denen jedes eine Perspektive auf die Szene repräsentiert. In aktuellen WebXR-Implementierungen wird die Liste niemals mehr als zwei Einträge enthalten: einen, der die Position und den Betrachtungswinkel des linken Auges beschreibt, und einen weiteren, der dasselbe für das rechte Auge tut. Sie können feststellen, welches Auge eine bestimmte XRView darstellt, indem Sie den Wert der eye-Eigenschaft überprüfen, die eine Zeichenfolge ist, deren Wert left oder right ist (ein dritter möglicher Wert, none, könnte theoretisch eventuell verwendet werden, um eine andere Sichtweise darzustellen, wird aber derzeit in der gesamten API nicht vollständig unterstützt).
Beispielrahmenrückruf
Ein ziemlich grundlegender (aber typischer) Rückruf zum Rendern von Frames könnte so aussehen:
function myAnimationFrameCallback(time, frame) {
const adjustedRefSpace = applyPositionOffsets(xrReferenceSpace);
const pose = frame.getViewerPose(adjustedRefSpace);
animationFrameRequestID = frame.session.requestAnimationFrame(
myAnimationFrameCallback,
);
if (pose) {
const glLayer = frame.session.renderState.baseLayer;
gl.bindFramebuffer(gl.FRAMEBUFFER, glLayer.framebuffer);
CheckGLError("Binding the framebuffer");
gl.clearColor(0, 0, 0, 1.0);
gl.clearDepth(1.0);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
CheckGLError("Clearing the framebuffer");
const deltaTime = (time - lastFrameTime) * 0.001;
lastFrameTime = time;
for (const view of pose.views) {
const viewport = glLayer.getViewport(view);
gl.viewport(viewport.x, viewport.y, viewport.width, viewport.height);
CheckGLError(`Setting viewport for eye: ${view.eye}`);
myRenderScene(gl, view, sceneData, deltaTime);
}
}
}
Der Rückruf beginnt mit dem Aufrufen einer benutzerdefinierten Funktion, applyPositionOffsets(), die einen Referenzraum übernimmt und seiner Transformationsmatrix alle nötigen Änderungen hinzufügt, die vorgenommen werden müssen, um Dinge wie Benutzereingaben von Geräten, die nicht von WebXR gesteuert werden, wie Tastatur und Maus, zu berücksichtigen. Der angepasste XRReferenceSpace, der von dieser Funktion zurückgegeben wird, wird dann in die XRFrame-Methode getViewerPose() übergeben, um die XRViewerPose zu erhalten, die die Position und den Betrachtungswinkel des Betrachters darstellt.
Der nächste Schritt ist das Anstehen der Anfrage, den nächsten Videoframe zu rendern, damit wir uns später nicht darum kümmern müssen, indem wir requestAnimationFrame() erneut aufrufen.
Jetzt ist es Zeit, die Szene zu rendern. Wenn wir eine Pose erfolgreich erhalten haben, beziehen wir die XRWebGLLayer, die für das Rendern verwendet wird, aus der renderState-Eigenschaft des baseLayer-Objekts der Sitzung. Wir binden dies über die WebGLRenderingContext-Methode gl.bindFrameBuffer() an das gl.FRAMEBUFFER-Ziel von WebGL.
Dann löschen wir den Framepuffer, um sicherzustellen, dass wir mit einem bekannten Zustand beginnen, da unser Renderer nicht jedes Pixel berührt. Wir setzen die Löschfarbe auf opakes Schwarz mit gl.clearColor() und den Wert, um den Tiefenpuffer auf 1.0 zu löschen, indem wir die WebGLRenderingContext-Methode gl.clearDepth() aufrufen. Dann rufen wir die WebGLRenderingContext-Methode gl.clear() auf, die den Framepuffer löscht (da wir gl.COLOR_BUFFER_BIT im Maskenparameter einbeziehen) und den Tiefenpuffer (weil wir gl.DEPTH_BUFFER_BIT einbeziehen).
Dann bestimmen wir, wie viel Zeit seit dem vorherigen gerenderten Frame vergangen ist, indem wir die gewünschte Zeit für das Rendern des Frames mit der Zeit des letzten gerenderten Frames vergleichen. Da dieser Wert in Millisekunden ist, konvertieren wir ihn in Sekunden, indem wir ihn mit 0.001 multiplizieren (bzw. durch 1000 dividieren).
Nun durchlaufen wir die Ansichten der Pose, wie sie im XRViewerPose-Array, views, gefunden wurden. Für jede Ansicht fragen wir die XRWebGLLayer nach dem geeigneten Sichtfenster, das verwendet werden soll, konfigurieren das WebGL-Sichtfenster entsprechend, indem wir Positions- und Größeninformationen in gl.viewport() übergeben. Dies beschränkt das Rendern so, dass wir nur in den Teil des Framepuffers zeichnen können, der das von view.eye identifizierte Bild repräsentiert.
Mit den so festgelegten Einschränkungen und allem anderen, was wir brauchen, bereit, rufen wir eine benutzerdefinierte Funktion, myRenderScene(), um tatsächlich die Berechnungen und das WebGL-Rendering zum Rendern des Frames durchzuführen. In diesem Fall übergeben wir den WebGL-Kontext 'gl', die XRView 'view', ein 'sceneData'-Objekt (das Dinge wie die Vertex- und Fragmentshader, Vertex-Listen, Texturen usw. enthält) und deltaTime, das angibt, wie viel Zeit seit dem vorherigen Frame vergangen ist, damit wir wissen, wie weit wir die Animation vorantreiben müssen.
Wenn diese Funktion zurückkehrt, hat der WebGL-Framepuffer, der von WebXR verwendet wird, jetzt zwei Kopien der Szene, jede belegt die halbe Ansicht: eine für das linke Auge und eine für das rechte Auge. Dies macht sich seinen Weg durch die XR-Software und Treiber in das Headset, wo jede Hälfte dem entsprechenden Auge gezeigt wird.