3D 碰撞检测
本文介绍了用于在 3D 环境中实现碰撞检测的不同包围体(bounding volume)技术。后续文章将讨论特定 3D 库中的实现。
轴对齐包围盒
在 2D 碰撞检测中,轴对齐包围盒(axis-aligned bounding box,AABB 包围盒)是判断两个物体是否重叠的最快算法。这种方法是将游戏实体包裹在一个非旋转的(因此是轴对齐的)盒中,并检查这些盒在三维坐标空间中的位置,以确定它们是否重叠。
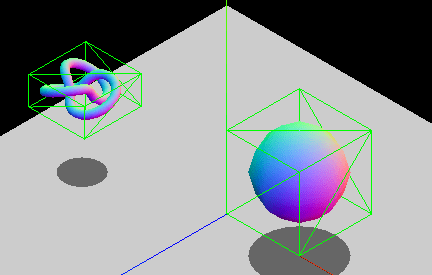
由于性能原因,其存在轴对齐约束。两个非旋转的盒子之间是否重叠可以只通过逻辑比较进行检查,而旋转的盒子则需要三角运算,计算速度较慢。如果你有旋转的物体,可以通过修改包围盒的尺寸,这样盒子仍可以包裹物体,或者选择使用另一种边界几何类型,比如球体(旋转不改变形状)。下面的 GIF 动画显示了 AABB 的图形示例,该示例调整其大小以适应旋转实体。盒子不断改变尺寸以紧密贴合内部的实体。
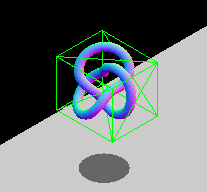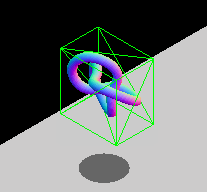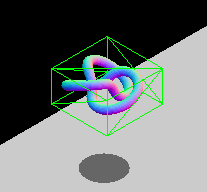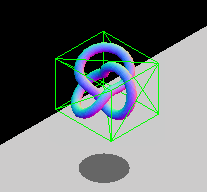
备注:参考使用 Three.js 的包围体,以了解该技术的实际实现。
点与 AABB
测试一个点是否在 AABB 内部非常简单——我们只需要测试这个点的坐标是否在 AABB 内(分别考虑每个坐标轴)。如果假设 Px、Py 和 Pz 是点的坐标,BminX–BmaxX、BminY–BmaxY 和 BminZ–BmaxZ 是 AABB 的每一个坐标轴的范围,我们可以使用以下公式计算两者之间的碰撞是否发生:
或者用 JavaScript:
function isPointInsideAABB(point, box) {
return (
point.x >= box.minX &&
point.x <= box.maxX &&
point.y >= box.minY &&
point.y <= box.maxY &&
point.z >= box.minZ &&
point.z <= box.maxZ
);
}
AABB 与 AABB
测试一个 AABB 是否和另一个 AABB 相交类似于测试点的方法。我们只需要基于每一条坐标轴测试盒子的边界。下图显示了我们基于 X 轴的测试——基本上是测试 AminX–AmaxX 和 BminX–BmaxX 是否重叠。

在数学上的表示就像这样:
在 JavaScript 中,我们可以这样:
function intersect(a, b) {
return (
a.minX <= b.maxX &&
a.maxX >= b.minX &&
a.minY <= b.maxY &&
a.maxY >= b.minY &&
a.minZ <= b.maxZ &&
a.maxZ >= b.minZ
);
}
包围球
使用包围球(bounding sphere)检测碰撞比 AABB 盒子稍微复杂一点,但仍旧相当容易。球体的主要优势是它的旋转不变性,如果包裹的实体旋转,包围球仍将是相同的。它的主要缺点是,除非包裹的实体实际上是球形的,否则包裹通常不太合适(比如用包围球包裹一个人将导致一些误报,而 AABB 盒子将更合适)。
点与球
测试是否一个球体包含一个点,我们需要计算点和球体的中心之间的距离。如果这个距离小于或等于球的半径,这个点就在球体内部。

两个点 A 和 B 之间的欧氏距离是 ,我们的公式指出,点与球体之间的碰撞检测应该像这样:
或者用 JavaScript:
function isPointInsideSphere(point, sphere) {
// 我们使用乘法是因为这样比调用 Math.pow 更快
const distance = Math.sqrt(
(point.x - sphere.x) * (point.x - sphere.x) +
(point.y - sphere.y) * (point.y - sphere.y) +
(point.z - sphere.z) * (point.z - sphere.z),
);
return distance < sphere.radius;
}
备注:上面的代码有一个平方根,计算开销可能很大。一种简单的优化是将平方距离与平方半径进行比较,以避免这种情况,所以优化后的不等式涉及 distanceSqr < sphere.radius * sphere.radius。
球体与球体
球体与球体的测试类似于点与球体的。我们需要测试的是球体的中心之间的距离小于或等于半径的总和。
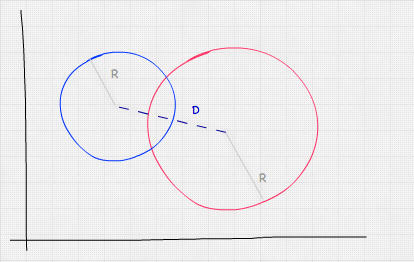
在数学上,应该像这样:
或者用 JavaScript:
function intersect(sphere, other) {
// 我们使用乘法是因为这样比调用 Math.pow 更快
const distance = Math.sqrt(
(sphere.x - other.x) * (sphere.x - other.x) +
(sphere.y - other.y) * (sphere.y - other.y) +
(sphere.z - other.z) * (sphere.z - other.z),
);
return distance < sphere.radius + other.radius;
}
球体与 AABB
测试一个球和一个 AABB 的碰撞是稍微复杂,但过程仍然简单和快速。一个合乎逻辑的方法是检查 AABB 每个顶点,计算每一个点与球的距离。然而这有点大材小用了,测试所有的顶点是不必要的,因为我们可以仅计算 AABB 的最近点(不一定是一个顶点)和球体的中心之间的距离,看看它是小于或等于球体的半径。我们可以通过逼近球体的中心和 AABB 的距离得到这个值:
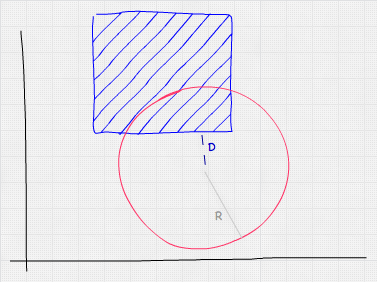
在 JavaScript 中,我们可以像这样进行测试:
function intersect(sphere, box) {
// 通过逼近距离获得距离球体中心最近的点
const x = Math.max(box.minX, Math.min(sphere.x, box.maxX));
const y = Math.max(box.minY, Math.min(sphere.y, box.maxY));
const z = Math.max(box.minZ, Math.min(sphere.z, box.maxZ));
// 这与 isPointInsideSphere 相同
const distance = Math.sqrt(
(x - sphere.x) * (x - sphere.x) +
(y - sphere.y) * (y - sphere.y) +
(z - sphere.z) * (z - sphere.z),
);
return distance < sphere.radius;
}
使用物理引擎
3D 物理引擎提供了碰撞检测算法,其中大多数也都是基于包围体。物理引擎的工作方式是创建一个物理体,通常附加到其可视化表示上。该物体具有诸如速度、位置、旋转、扭矩等属性,还有一个物理形状。这个形状是碰撞检测计算中考虑的形状。
我们准备了一个碰撞检测演示(源代码),你可以看到这些技术是如何运作的——这里使用了开源的 3D 物理引擎 cannon.js。
参见
MDN 上的相关文章:
外部资源: